Sorted Trie Insertion

This document describes the algorithm implemented in crates/common/trie/trie_sorted.rs which is used to speed up the insertion time in snap sync. During that step we are inserting all of the accounts state and storage slots downloaded into the Ethereum world state Merkle Patricia Trie. To know how that trie works, it's recommended to read this primer first.

Concept

Naive algorithm: we insert keys in arbitrary (unsorted) order. This version requires O(n*log(n)) reads and writes to disk. This is because each insertion creates a new leaf, which modifies the hash of its parent branch recursively. We could avoid reads to disk by having the trie in memory, but this is unviable for large amounts of state data.

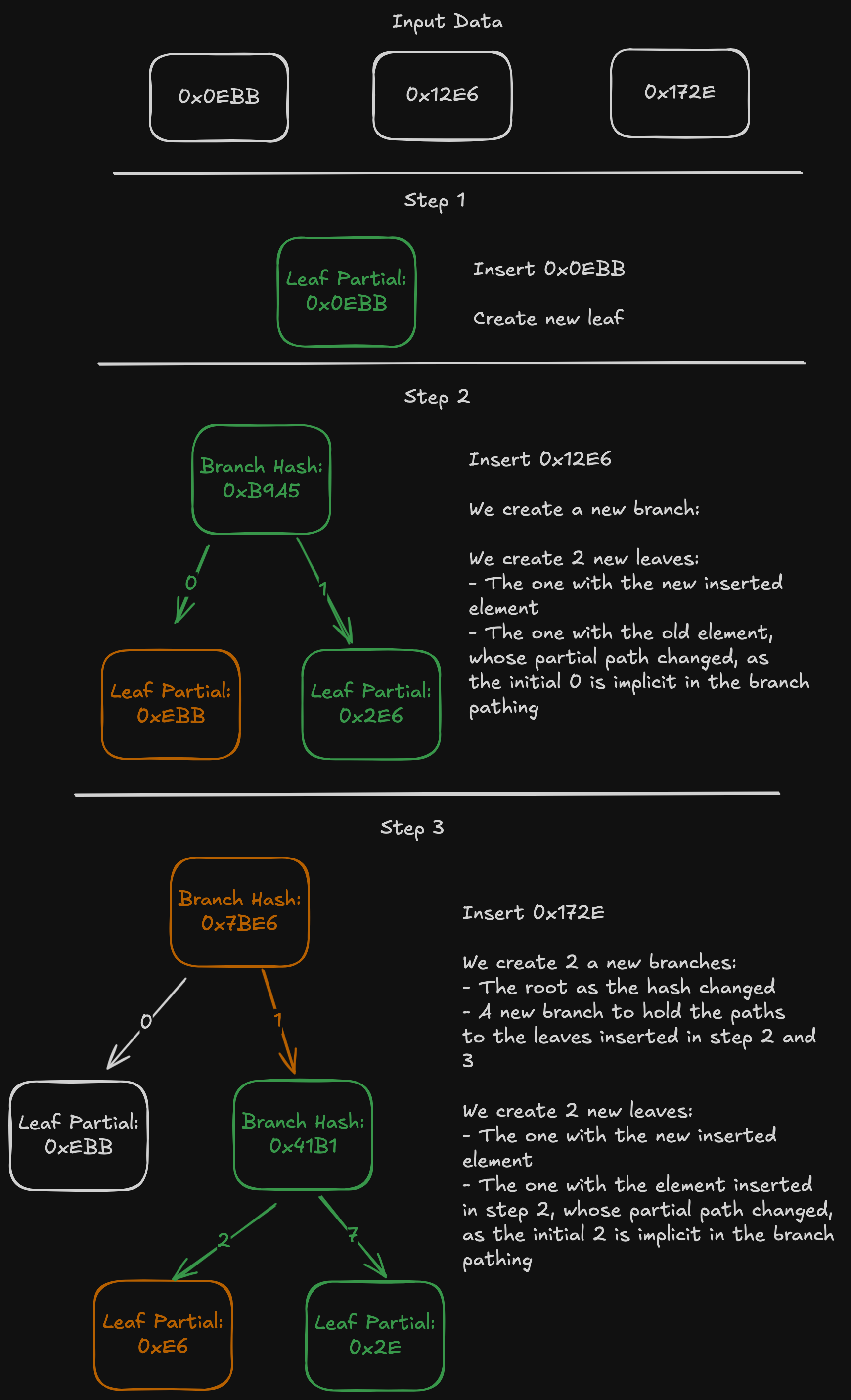
Example of the Naive implementation: Image showing the insertion of 3 elements 0x0EBB, 0x12E6, 0x172E. Each one requiring multiple new reads and writes

If the input data is sorted, the computation can be optimized to be O(n). In the example, just by reading 0x0EBB and 0x172E, we know that there is a branch node as root (because they start with different nibbles), and that the leaf will have a partial path of 0xEBB (because no node exists between 0x0EBB and 0x172E if it's sorted). The root branch node we know exists and will be modified, so we don't write until we have read all input.

Implementation

The implementation maintains three pointers:

The current element being processed.
The next input value.
The parent of the current element.

All parents that can still be modified are stored in a "parent stack". Based on these, the algorithm can determine the next write operation to perform.

Scenarios

Depending on the state of the three current pointers, one of 3 scenarios can happen:

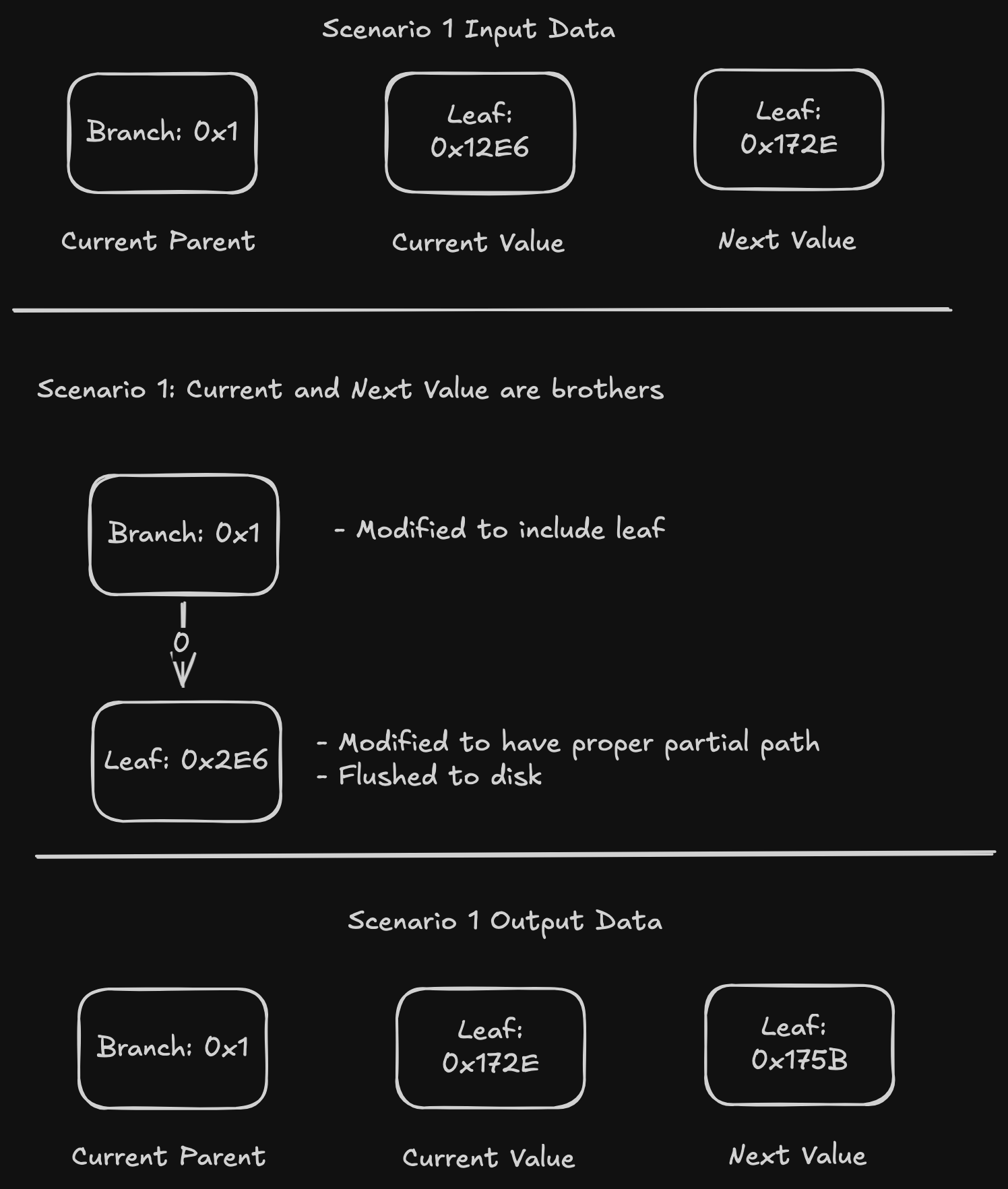
Scenario 1: Current and next value are siblings with the current parent being the parent of both values. This happens when the parent and both values share the same number of nibbles at the beginning of their paths. In our example, all node paths start with 0x1 and then diverge.

In this scenario, we can compute the leaf for the current value, write it, update the parent to include a pointer to that leaf, and then continue.

Image showing the insertion of 1 element with a current parent branch 0x1, the current element 0x12E6 and next element 0x172E. 0x12E6 is inserted with a single write

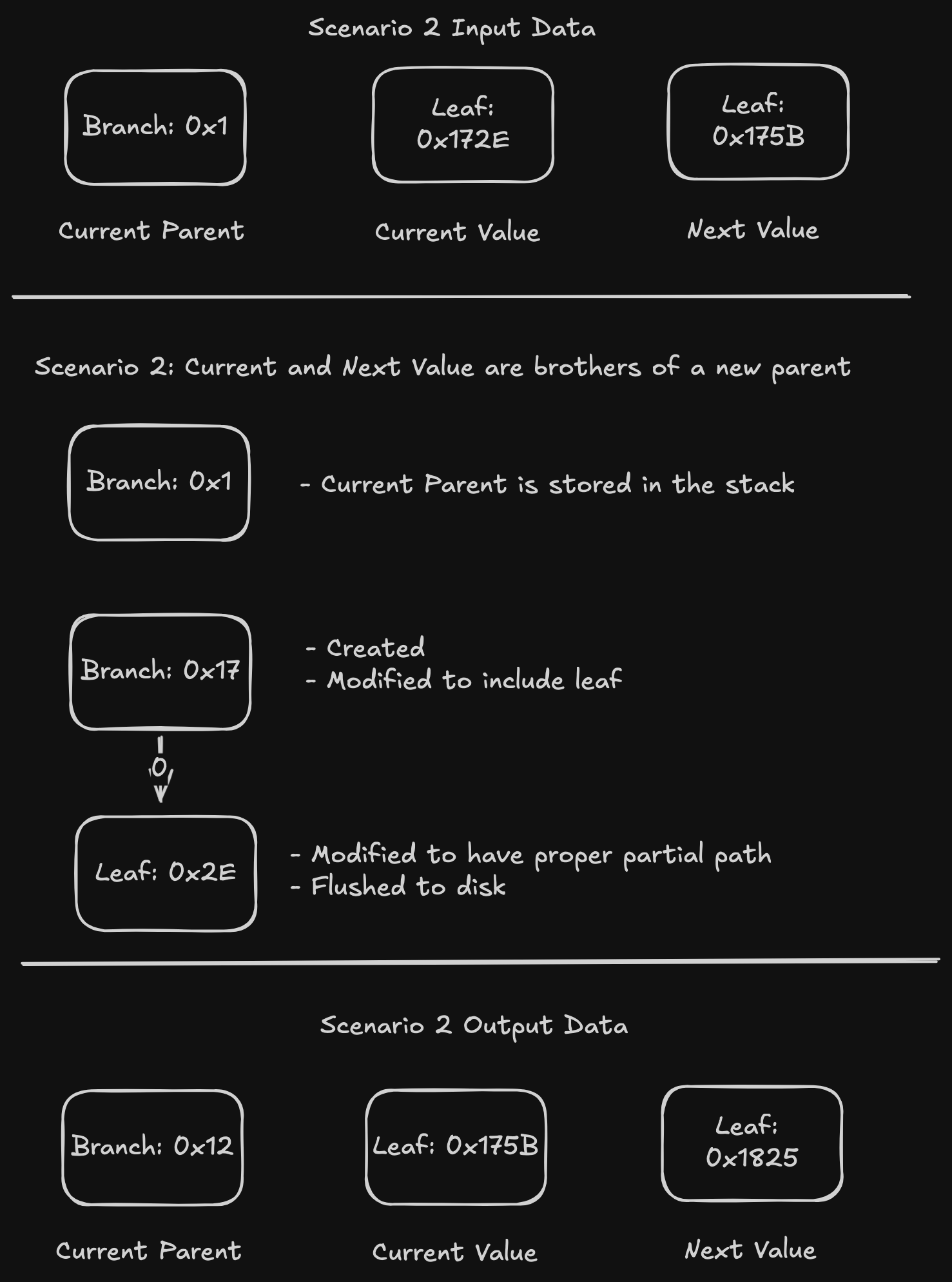
Scenario 2: Current and next values are siblings of a new current parent. This happens when the parent shares less nibbles from their paths than what the siblings share. In our example, the current and next value share 0x17, while the parent only shares 0x1.

In this scenario, we know the leaf we need to compute from the current value so we write that. Furthermore, we know that we need a new branch at 0x17, so we create it and insert the leaf we just computed and insert into the branch. The current parent is stored in the "parent stack", and the new branch becomes the current parent.

Image showing the insertion of 1 element with a current parent branch 0x1, the current element 0x172E and next element 0x175B. 0x172E is inserted with a single write, while the current parent branch is put onto the stack, and a new current parent branch 0x17 is created

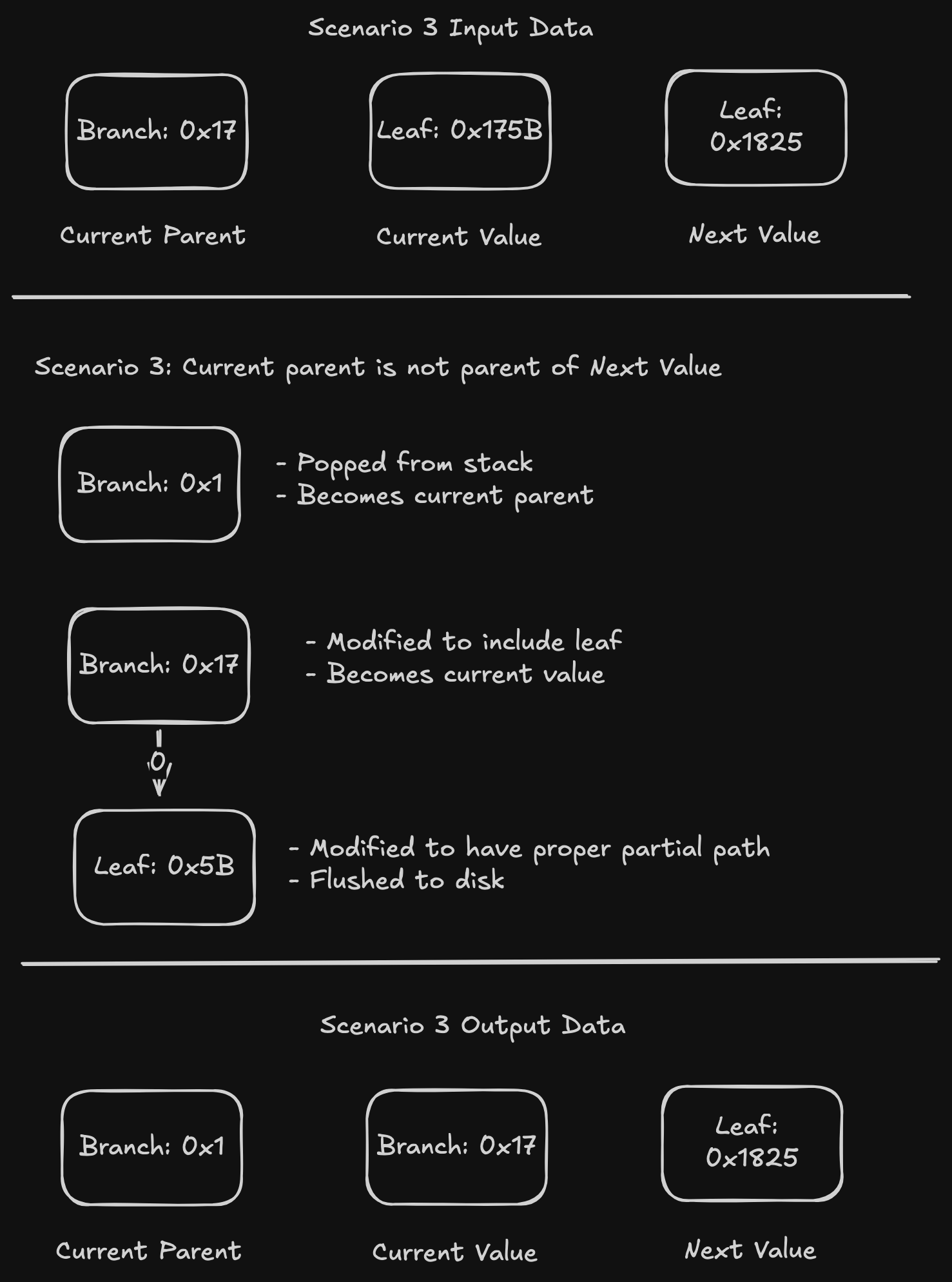
Scenario 3: The current parent is not the parent of the next value. This happens when the parent doesn't have all of the nibbles of its path.

In this scenario, we know the leaf we need to compute from the current value, so we write that. We change the current value to be the current parent, and the new current parent is popped from the "parent stack".

Image showing the insertion of 1 element with a current parent branch 0x17, the current element 0x175B and next element 0x1825. 0x175B is inserted with a single write, while the current parent branch becomes the current value, and the current parent branch is popped from the stack

These three scenarios keep repeating themselves until the trie is complete, at which point the algorithm returns a hash to the root node branch.

Inserting with extensions

In general, each write to disk is prepared to properly handle extensions as the write function knows what it's writing and what was its parent and full path. As such, it can check if the insertion is a branch and if an extension is needed.

A specific edge case is the root node, which is assumed to always be a branch node, but the code has a special case check to see if the root node has a single child, in which case it changes to an extension or leaf as needed, while modifying the other nodes in the trie.

Concurrency

The slowest step in this process is flushing nodes to disk. To avoid stalling during writes, the algorithm uses an internal buffer that holds a fixed number of nodes. Once the buffer is filled, it creates a new task that writes it to disk in the background.

We want to limit the amount of buffers we can have, so we allocate a fixed number of buffers at the beginning and we use a channel for the algorithm to receive empty buffers and the writing task clears the buffer and sends it back through the channels.

These tasks are executed using a custom thread pool defined in /crates/concurrency/concurrency.rs